مخطط أسبوعي

  • TP Analyse numérique 02

    طي الكل توسيع الكل

  • La présentation de l'auteur

    • Dr: Nour El-houda BOUCHERCHEM.
    • Département des Mathématiques.
    • Faculté des Sciences.
    • Université de 20 Août 1955-SKIKDA.
    • Email: n.boucherchem@univ-skikda.dz
    • Disponibilité : Au bureau : Dimanche, lundi de 12h30 -14h00.
                                                     

  • Information sur le cours

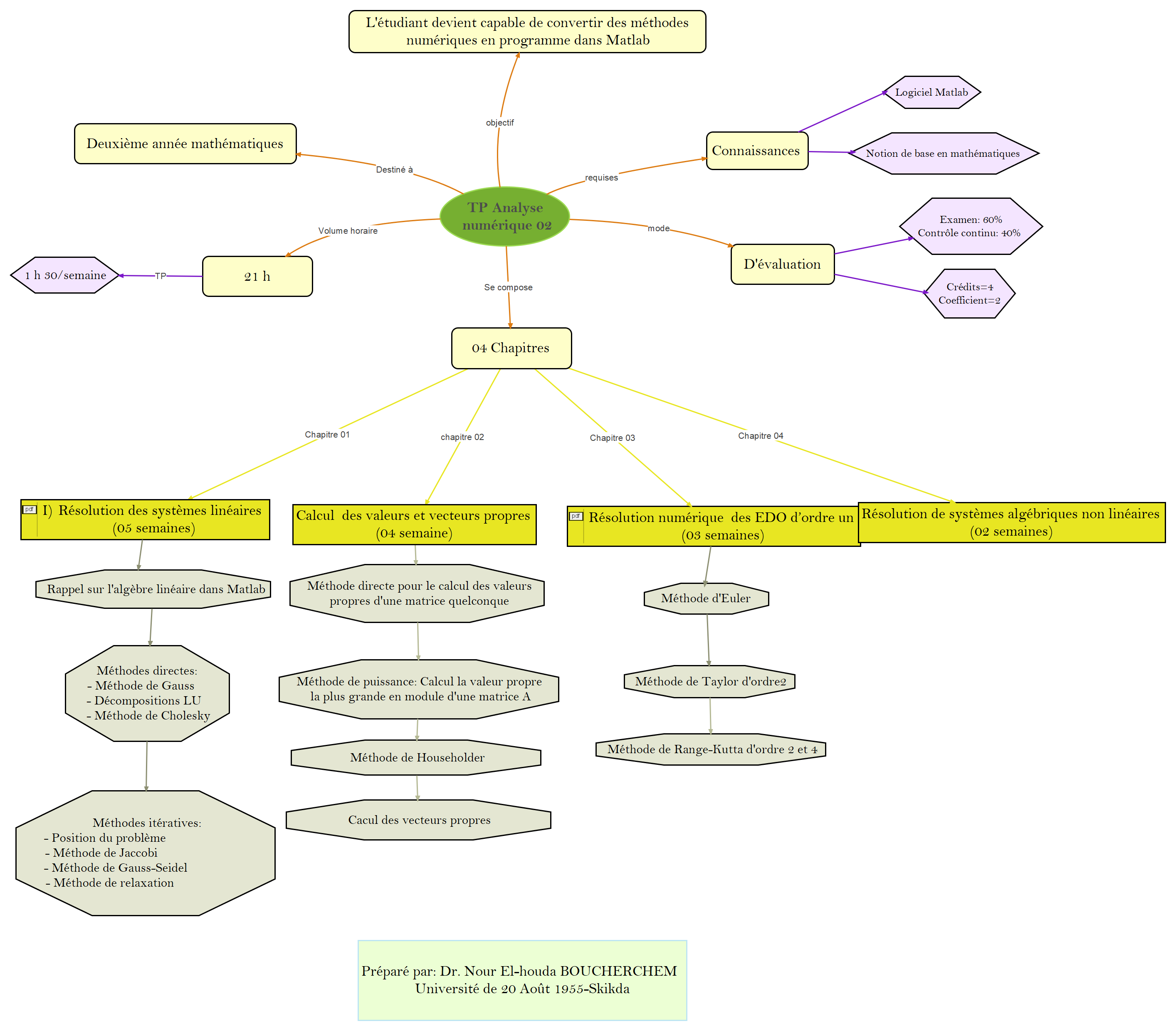
    • Intitulé du cours: TP Analyse Numérique 02.
    • Département: Mathématiques.
    • Facultés: Sciences.
    • Université: 20 Août 1955-Skikda.
    • Public cible : 2ème année License mathématiques.
    • Crédit : 04.

    • Coefficient : 02.
    • Durée : 14 semaines.
    • Horaire : Dimanche : 09h30-11h00.
                      Lundi : 08h00-09h30.
    • Salle : TP05.
    • Evaluation: 60% Examen, 40% Contrôle Continue. 
                                  

  • Plan Global

    1. Objectifs du cours.
    2. Prérequis.
    3. Test de prérequis.
    4. Introduction.
    5. Chapitre 01: Résolution des systèmes linéaires.
    6. Chapitre 02: Résolution numérique des EDO d’ordre un.
    7. Test de sortie.
    8. Bibliographie.

  • Objectifs du cours

    Nous aurons durant ce module aborder la dérivation des algorithmes pour résoudre

    •  les systèmes linéaires de la forme Ax=b par des méthodes directes et itératives 
    •  les EDO d'ordre un.

         

  • Prérequis

    Pour aborder efficacement le TP d'analyse numérique 02 utilisant le logiciel MATLAB, l'étudiant doit disposer de connaissances préalables à la fois en programmation MATLAB et en mathématiques.

    1.    Prérequis en mathématiques : Les bases nécessaires pour comprendre et appliquer les méthodes numériques sont :

    • Algèbre linéaire. 
    • Analyse. 

    2.    Prérequis en programmation (MATLAB) : Il est essentiel de maîtriser les éléments fondamentaux de MATLAB, notamment :

    • Base du langage MATLAB.
    • Outils utiles.

                                                                    

  • Test de Prérequis


  • Introduction

    L’analyse numérique est une discipline qui fournit des outils et méthodes pour résoudre, de manière approchée, des problèmes mathématiques dont la solution exacte est difficile ou impossible à obtenir analytiquement. Ce TP a pour objectif de familiariser l’étudiant avec la mise en œuvre de ces méthodes, tout en évaluant leur précision, leur stabilité et leur efficacité.

    Il se compose de deux chapitres complémentaires :

    • La résolution des systèmes linéaires, élément central en modélisation scientifique, permettant de traiter de grands ensembles d’équations interdépendantes.

    • La résolution des équations différentielles ordinaires (EDO) d’ordre un, indispensables pour décrire l’évolution temporelle de phénomènes physiques, biologiques ou économiques.

    À travers ces deux volets, l’étudiant acquiert à la fois une compréhension théorique des méthodes et une expérience pratique de leur application, notamment grâce à l’utilisation d’outils informatiques de calcul :"MATLAB".


  • Chapitre 01: Résolution des systèmes linéaires

    La résolution des systèmes d’équations linéaires est une étape fondamentale dans de nombreuses applications scientifiques et techniques. Ce chapitre présente les méthodes numériques permettant d’obtenir des solutions fiables, qu’elles soient directes ou itératives. L’accent est mis sur la précision, la stabilité et l’efficacité des calculs.

  • Chapitre 02: Résolution numérique des EDO d'ordre un

    Les équations différentielles d’ordre un interviennent dans la modélisation de phénomènes physiques, chimiques, biologiques et économiques. Ce chapitre explore les méthodes numériques permettant d’en approcher les solutions lorsque la résolution analytique est difficile, en particulier les schémas d’Euler, de Taylor et de Runge-Kutta. L’objectif est d’analyser la convergence et la stabilité de ces méthodes tout en mettant l’accent sur leur mise en œuvre pratique.

  • Test de sortie

  • Bibliographie

    • Ph. G. Ciarlet : Introduction à l'analyse numérique matricielle et à l'optimisation, Dunod, Paris 1998.
    • Curtis F. Gerald, P. O. Wheatdey : Applied Numerical Analysis, Addison-Wesley Pub. Company.
    • J. Ph. Grivet : Méthodes numériques appliquées : Pour le scientifique et l'ingénieur, EDP SCIENCES, 2009.
    • Y. Meddahi : Travaux Pratiques Méthodes Numériques, Polycopié Pédagogique, Université Hassiba Benbouali de Chlef, Année Universitaire 2018 - 2019.
    • J. Rappaz, M. Picasso : Introduction à l'analyse numérique, Presses Polytechniques et Universitaires
    • Romandes (PPUR), 1997.
    • F. Zemani : Programmation et méthode numérique sous MATLAB, Polycopié, Université des Sciences et de la Technologie d'Oran Mohamed Boudiaf.